APY Calculator

How APY Calculator Works?

This APY Calculator is a comprehensive tool designed to help users calculate and understand the relationship between Annual Percentage Rate (APR), Annual Percentage Yield (APY), and investment growth over time. Here’s a breakdown of its functionality:

1. Input Collection:

The calculator collects the following information from the user:

2. APR to APY Conversion:

The calculator converts the provided APR to APY using the formula: APY = (1 + r/n)^n – 1 Where:

3. APY to APR Conversion:

The calculator can also perform the reverse calculation, converting APY to APR if the user provides the APY instead.

4. Future Balance Calculation:

5. Interest Calculation:

The calculator determines the total interest earned over the investment period.

6. Results Display:

The calculator provides the following outputs:

Additional Features of APY Calculator:

1. Flexible Time Inputs:
   • The calculator allows users to input the term in various units (Years, Months, Weeks, or Days), providing flexibility for different investment scenarios.
2. Real-time Calculations:
   • As users adjust any input, the calculator immediately recalculates and updates all results.
3. Reverse Calculations:
   • Users can input either APR or APY, and the calculator will determine the other value.
   • This feature allows for easy comparison between different investment options that may be advertised using either APR or APY.

This versatile APY Calculator adapts to various user needs, whether they’re planning long-term investments, comparing different savings accounts, or analyzing the impact of compound interest over different time periods. Its comprehensive inputs and outputs make it a valuable tool for both personal financial planning and professional investment analysis.

What is APY?

APY stands for Annual Percentage Yield. APY represents the total amount of interest you can earn on your money over a year, considering the effects of compounding interest. Regular simple interest pays only on the original deposit, but APY considers how interest accumulates on the principal and generates increased earnings.

To put it simply, APY is the “total package” that shows us how much we’ll earn in a year, considering how often the interest is added to our account. This makes it an essential tool for comparing different savings options and understanding our potential returns.

APY Definition

APY is the amount of interest you can earn over a year including compounding interest on the money you save or invest in banks or other money markets. The higher the APY, the more interest you can earn.

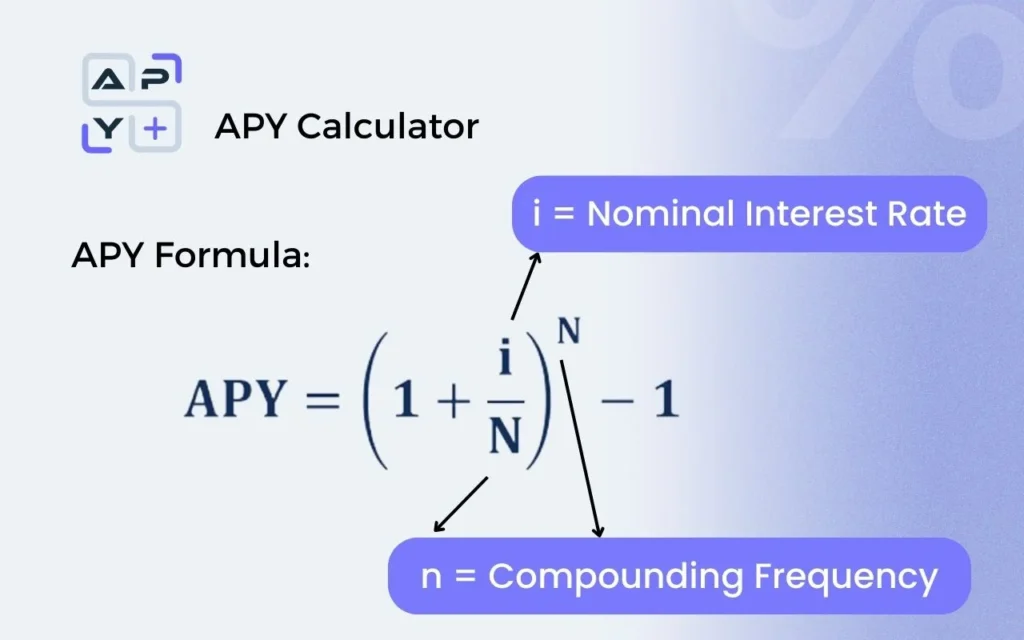
APY Calculation Formula

The APY calculation uses this formula:

Example Calculation

What is Compound Interest? How it’s Calculated

Money grows through “interest on interest” with compound interest. Simple interest pays only on the principal amount, but compound interest makes money grow faster by generating returns on both the original deposit and accumulated interest.

Compound Interest Formula

The compound interest calculation uses this formula:

What are Compounding Frequencies?

Returns change substantially based on how often interest compounds. A USD 10,000 deposit at 5.25% interest over one year shows these returns with different compounding periods:

Compounding Frequency	Interest Rate	APY Rate	Annual Return (APY)
Annually	5.25%	5.25%	USD 525.00
Monthly	5.25%	5.38%	USD 537.82
Daily	5.25%	5.39%	USD 538.99

How Compounding Affects APY

The frequency of compounding effects our APY directly. More frequent compounding leads to earnings above the stated interest rate. A 4% interest rate that compounds monthly yields an APY of about 4.07%, while daily compounding pushes it to 4.08%. This gap becomes more noticeable as time passes, which shows why investors should look at both interest rates and compounding frequency before choosing financial products.

Difference between APY and APR

The difference between APR (Simple Interest) and APY plays a significant role in making smart financial decisions. These two rates serve different purposes and work in distinct ways.

What is APR Interest?

Annual Percentage Rate (APR) shows how much it costs to borrow money each year, including interest and certain fees. APR uses simple interest calculations that don’t factor in compounding effects, unlike APY.

Common APR applications include:

• Credit cards and personal loans
• Mortgages and auto loans
• Home equity lines of credit

APY vs APR: Key Differences

These rates handle interest calculations differently. Here’s a clear comparison:

Feature	APR	APY
Interest Type	Simple	Compound
Primary Use	Borrowing costs	Investment returns
Rate Display	Usually lower	Usually higher
Fee Inclusion	May include fees	Interest only

When to Focus on APY vs APR

APR matters most with borrowed money because it reveals the true cost of loans. Lower APR means less money spent on interest and fees. APY becomes more relevant for investments and savings since it shows the actual earnings potential with compound interest.

Interest compounding can substantially affect total costs in credit products. Lenders must disclose both rates under the Truth in Lending Act, which helps consumers make smarter choices about financial products.

Fixed vs Variable APY

The way we earn money from financial products largely depends on two different types of APY that affect our returns by a lot. Let’s look at how fixed and variable APYs work across various banking products.

What is Fixed APY?

Fixed APY gives us a guaranteed rate of return that doesn’t change during a specific term. You’ll mostly find fixed APYs in Certificate of Deposit (CD) accounts where your money stays put for a set time. These accounts come with some clear advantages:

• Your returns stay the same whatever the market does
• The rates are usually higher than variable-rate accounts
• You’re protected if interest rates drop

It’s worth mentioning that fixed APY accounts need your money locked away for a specific period, and you’ll pay penalties if you take it out early.

What is Variable APY?

The market conditions and changes in the federal funds rate make variable APY go up and down. Most savings and checking accounts use variable APYs. Here’s a quick comparison between variable and fixed APYs:

Feature	Fixed APY	Variable APY
Rate Changes	Stays constant	Fluctuates with market
Access to Funds	Limited/Penalties	Flexible access
Typical Products	CDs	Savings/Checking accounts
Risk Level	Predictable	Market dependent

Variable APY accounts work great if interest rates climb but give you lower returns when rates fall. The Federal Reserve’s decisions play a big role here – your variable APYs tend to follow their federal funds rate changes up or down.

A high-yield savings account might start you off at 4% APY that could jump to 4.5% or drop to 3.5% based on what the market does. Some banks try to attract customers with promotional fixed APYs – like 5% on your first $500 – before switching to their regular variable rate for anything extra you deposit.

APY Across Financial Products

Let me show you the APY differences between financial products and what you can expect to earn from each one.

1. Savings Accounts

Traditional savings accounts give you variable APYs of 0.45% on average, but you can get up to 5.50% with high-yield saving accounts options. These accounts let you access your money easily and still earn good returns, especially from online banks.

2. Checking Accounts

Standard checking accounts pay a tiny 0.07% APY. You can find high-yield checking accounts that pay up to 4.62%. But you’ll need to meet certain conditions like using your debit card enough times or setting up direct deposits.

3. Certificate of Deposit (CDs)

CDs give you some of the best fixed APYs among regular banking products. Here are the current rates:

CD Term	Typical APY Range
8-month	Up to 5.50%
1-year	4.50-5.00%
3-5 year	3.50-4.00%

4. Money Market Account

Money market accounts pay 0.64% on average nationwide. The best accounts offer rates between 4.90-5.00% APY. You get high yields plus the bonus of writing checks and using a debit card.

5. APY in Crypto

Crypto APY is different from regular banking products in several ways:

• You earn interest in cryptocurrency instead of dollars
• Rates are much higher but come with more risk
• You can earn through staking, yield farming, and liquidity provision
• Interest compounds more often, usually every seven days
• Market swings and token inflation rates can change your returns