Compound Interest Frequencies: Daily, Monthly, Quarterly, Semi-Annually and Annually

Are you looking to maximize your investment returns or understand how your savings grow over time? Understanding compounding frequencies is key to making informed financial decisions. This article breaks down the concept of compounding and explains how different frequencies—daily, weekly, monthly, quarterly, semi-annually, and yearly—impact your money’s growth.

Imagine you have a plant. The more often you water it, the faster it grows. Compounding is like watering your money. The more frequently you add interest (like water) to your money, the faster it grows.

• Daily compounding: Watering every day.
• Monthly compounding: Watering once a month.
• Quarterly compounding: Watering every three months.
• Yearly compounding: Watering once a year.

The more often you water (compound), the bigger and healthier your plant (money) will grow.

What is Compound Interest?

Compounding: The process of earning interest on both your initial investment (principal) and the interest earned over time.

Types of Compounding Frequencies:

How compound interest works

To understand how compound interest works, let’s consider an example. Imagine depositing USD 100.00 into a savings account that pays compound interest at a rate of 5% annually. After the first year, you would earn USD 5.00 in interest on your original investment, bringing your account balance to USD 105.00. In the second year, you would earn interest not only on your initial USD 100.00 but also on the USD 5.00 interest earned in the first year. This means you would earn USD 5.25 in interest after two years, bringing your total balance to USD 110.25.

The power of compound interest becomes more evident over longer periods. As time passes, the interest earned on the accumulated interest grows, creating a snowball effect. This is why compound interest is often referred to as “magical” – it has the potential to accelerate wealth growth significantly.

The frequency of compounding also plays a crucial role in how compound interest works. Compounding can occur annually, semi-annually, quarterly, monthly, or even daily. The more frequent the compounding, the faster the money grows. For instance, an account that compounds interest daily will grow faster than one that compounds annually, even if they have the same interest rate.

To calculate compound interest, a specific formula is used:

A = P(1 + r/n)^(nt)

Where: A = the final amount P = the principal (initial investment) r = the annual interest rate (in decimal form) n = the number of times interest is compounded per year t = the number of years

This formula allows for the calculation of the total amount after a certain period, taking into account the compounding effect.

The Rule of 72 is a useful tool related to compound interest. It provides a quick way to estimate how long it will take for an investment to double at a given interest rate. By dividing 72 by the annual interest rate, you can approximate the number of years it will take for the investment to double.

Compound interest 8th Wonder of the World has a significant influence on various financial products and decisions. It’s commonly used in savings accounts, certificates of deposit (CDs), and investment accounts. However, it’s important to note that compound interest can also work against you when it comes to loans and credit card debt, where interest can accumulate rapidly if not paid off promptly.

Compound Interest Frequencies

Compound interest frequencies refer to how often interest is calculated and added to the principal amount in an investment or loan. The frequency of compounding has a significant impact on the overall growth of an investment or the total amount owed on a loan. Different compounding frequencies can lead to varying results, even with the same interest rate and principal amount.

Daily compounding

Daily compounding is a type of interest calculation where interest is added to the principal every day. This is one of the most frequent compounding methods, resulting in the highest effective annual yield for a given interest rate.

Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With daily compounding, the interest would be calculated 365 times a year (assuming a non-leap year).

• Daily rate: The daily interest rate would be approximately 0.0137% (5% / 365 days).
• Calculation: The formula for daily compounding is A = P(1 + r/n)^(n*t), where A is the final amount, P is the principal, r is the annual interest rate, n is the number of times interest is compounded per year (365 in this case), and t is the number of years.

At the end of the year, your total balance would be $5,000 * (1 + 0.05/365)^365 = $5,256.32.

Weekly compounding

Weekly compounding is a type of interest calculation where interest is added to the principal once a week. This method provides more frequent compounding than monthly or quarterly, but less than daily.

Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With weekly compounding, the interest would be calculated 52 times a year.

• Weekly rate: The weekly interest rate would be approximately 0.0962% (5% / 52 weeks).
• Calculation: Using the compound interest formula A = P(1 + r/n)^(n*t), where n is 52 in this case.

At the end of the year, your total balance would be $5,000 * (1 + 0.05/52)^52 = $5,256.08.

Monthly compounding

Monthly compounding is a type of interest calculation where interest is added to the principal once a month. This is a common compounding frequency used by many financial institutions for savings accounts and certificates of deposit.

Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With monthly compounding, the interest would be calculated 12 times a year.

• Monthly rate: The monthly interest rate would be approximately 0.4167% (5% / 12 months).
• Calculation: Using the compound interest formula A = P(1 + r/n)^(n*t), where n is 12 in this case.

At the end of the year, your total balance would be $5,000 * (1 + 0.05/12)^12 = $5,255.85.

Quarterly compounding

Quarterly compounding is a type of interest calculation where interest is added to the principal four times a year, typically every three months. This method is less frequent than monthly compounding but more frequent than semi-annual or annual compounding.

Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With quarterly compounding, the interest would be calculated 4 times a year.

• Quarterly rate: The quarterly interest rate would be 1.25% (5% / 4 quarters).
• Calculation: Using the compound interest formula A = P(1 + r/n)^(n*t), where n is 4 in this case.

At the end of the year, your total balance would be $5,000 * (1 + 0.05/4)^4 = $5,254.41.

Semi-Annually Compounding

Semi-annual compounding is a type of interest calculation where interest is added to the principal twice a year. This means the interest is calculated and added to the balance every six months. While it’s not as frequent as daily or weekly compounding, it still provides a significant advantage over annual compounding.

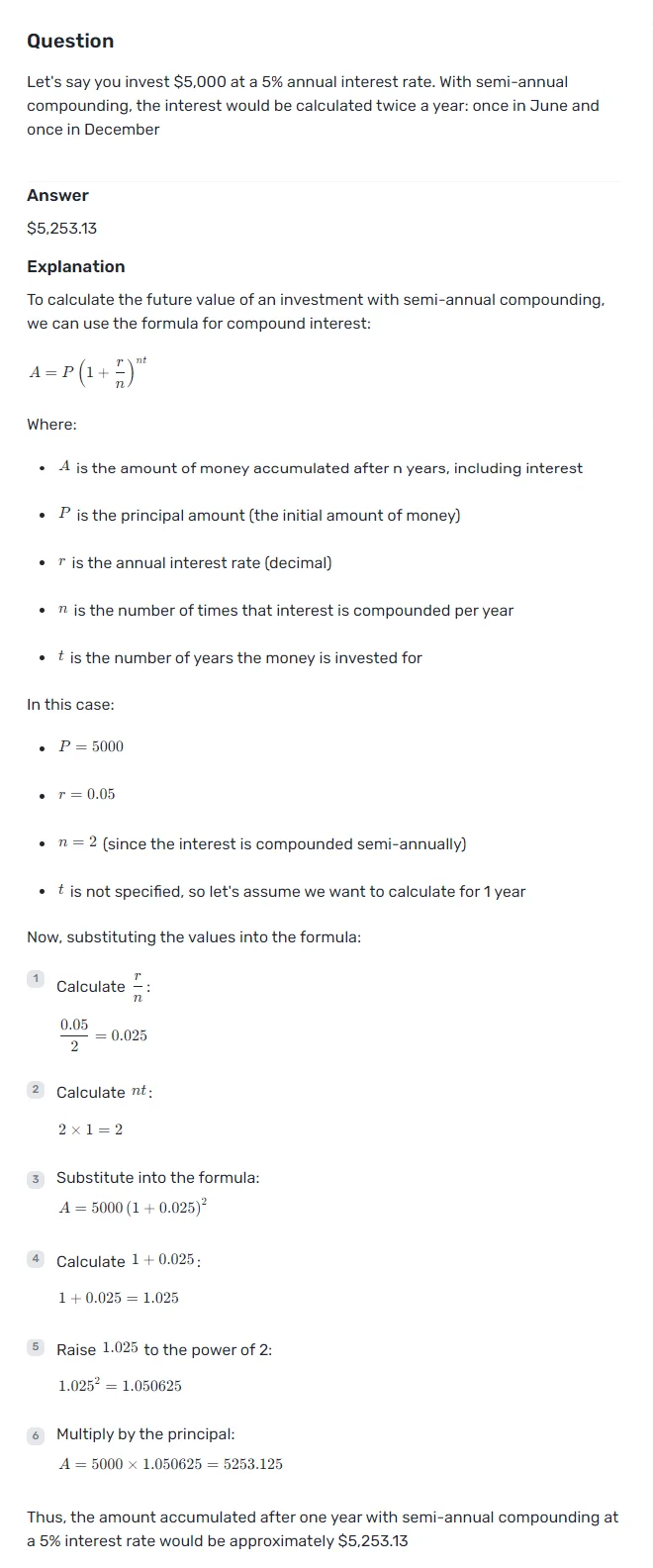
Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With semi-annual compounding, the interest would be calculated twice a year: once in June and once in December.

• First six months: The interest rate for six months would be 2.5% (5% annual rate divided by 2). So, the interest earned would be $5,000 * 2.5% = $125.
• Second six months: The interest is calculated on the new balance of $5,125. So, the interest earned would be $5,125 * 2.5% = $128.13.

At the end of the year, your total balance would be $5,000 + $125 + $128.13 = $5,253.13.

Annual compounding

Annual compounding is a type of interest calculation where interest is added to the principal once a year. This is the least frequent compounding method among those commonly used and results in the lowest effective annual yield for a given interest rate.

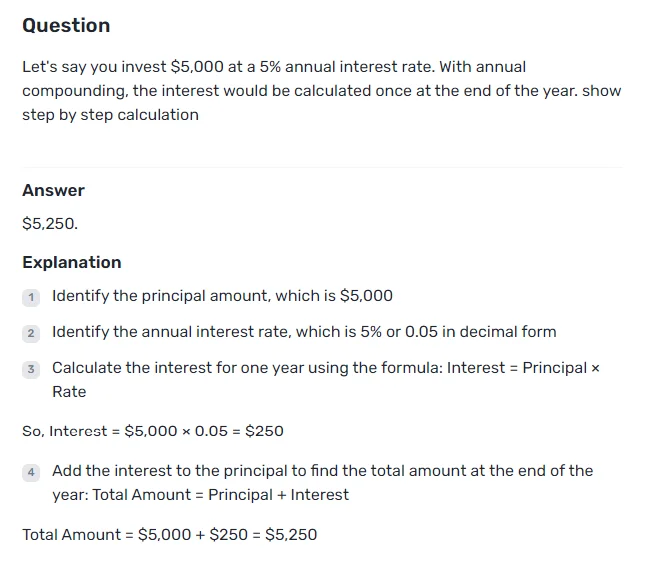
Example:

Let’s say you invest $5,000 at a 5% annual interest rate. With annual compounding, the interest would be calculated once at the end of the year.

• Annual rate: The annual interest rate is simply 5%.
• Calculation: Since the interest is compounded only once, we can use the simple interest formula: A = P(1 + r*t), where t is 1 for one year.

At the end of the year, your total balance would be $5,000 * (1 + 0.05) = $5,250.00.

Comparing Different Compounding Frequencies

Impact on investment growth

The frequency of compounding has a significant influence on investment growth. Generally, the more frequent the compounding, the more interest an investor earns. This is because interest is calculated and added to the principal more often, creating a larger base for future interest calculations. For instance, daily compounding allows for faster growth compared to annual compounding, even with the same interest rate and principal amount.

The effect of compounding depends on three main factors: investment horizon, rate of return, and compounding frequency. A longer investment horizon allows more time for interest to accumulate on interest, leading to greater wealth accumulation. Similarly, a higher rate of return results in more substantial growth over time. Compounding frequency, which is the interval at which interest multiplies, plays a crucial role in determining the overall growth of an investment.

Examples with calculations

To illustrate the impact of different compounding frequencies, let’s consider some examples with calculations:

1. Annual vs. Daily Compounding: Suppose an investor deposits USD 10000.00 in a savings account with a 4% annual interest rate. After 30 years:

• With annual compounding, the balance would be approximately USD 32434.00
• With daily compounding, the balance would grow to USD 33199.00

The difference of USD 765.00 demonstrates the advantage of more frequent compounding.

2. Various Compounding Frequencies: Consider an investment of USD 1000000.00 earning 20% per year over one year:

• Annual compounding: USD 1200000.00
• Semiannual compounding: USD 1210000.00
• Quarterly compounding: USD 1215506.00
• Monthly compounding: USD 1219391.00
• Daily compounding: USD 1221336.00

As the compounding frequency increases, the future value grows, but the incremental gain diminishes with each increase in frequency.

3. Continuous Compounding: The limit of compounding frequency is known as continuous compounding, calculated using the formula: FV = P × e^(rt) Where e is approximately 2.7183, r is the interest rate, and t is time.

Using the previous example, continuous compounding would result in a future value of USD 1221404.00, slightly higher than daily compounding.

When frequency matters most

Compounding frequency becomes particularly important in certain situations:

1. Long-term investments: The impact of compounding frequency is more pronounced over longer periods. For young investors saving for retirement, starting early with frequent compounding can lead to substantial growth over time.
2. High interest rates: When interest rates are higher, the difference between compounding frequencies becomes more significant.
3. Large principal amounts: With larger investments, even small differences in compounding frequency can result in substantial monetary differences.
4. Regular contributions or withdrawals: Compounding frequency can be especially important when regularly adding to or withdrawing from an account. For example, if USD 10000.00 is deposited over five years (USD 2000.00 each year) instead of upfront, the balance after 30 years would be about USD 30000.00, roughly USD 2500.00 less than when the full amount is deposited initially.
5. Loans and debts: For borrowers, less frequent compounding is preferable as it results in lower overall interest charges.

It’s worth noting that while compounding frequency can have a noticeable impact, its effect is limited. The difference between daily and continuous compounding, for instance, is often negligible in practical terms. Additionally, for small interest rates or short time periods, the impact of compounding frequency may be minimal.

Understanding these nuances of compound interest frequencies enables investors to make more informed decisions about their savings and investment strategies, potentially maximizing their long-term financial growth.

Conclusion

Compound interest frequencies have a significant influence on long-term savings and investments. The power of compounding, whether daily, weekly, monthly, quarterly, or annually, can lead to substantial differences in wealth accumulation over time. Understanding these different frequencies enables individuals to make informed decisions about their financial strategies, potentially maximizing their returns on savings and investments while minimizing borrowing costs.

To sum up, the impact of compound interest becomes more pronounced with higher interest rates, larger principal amounts, and longer investment horizons. While more frequent compounding generally leads to faster growth, it’s crucial to consider other factors such as fees, accessibility, and personal financial goals when choosing investment vehicles. By grasping these concepts, individuals can better navigate the financial landscape and work towards achieving their long-term financial objectives.

FAQs